IPUMS NHGIS – Use It for Good

Measuring Food Security with U.S. Federal Data

October 20, 2025October 10, 2025 by mpcblog

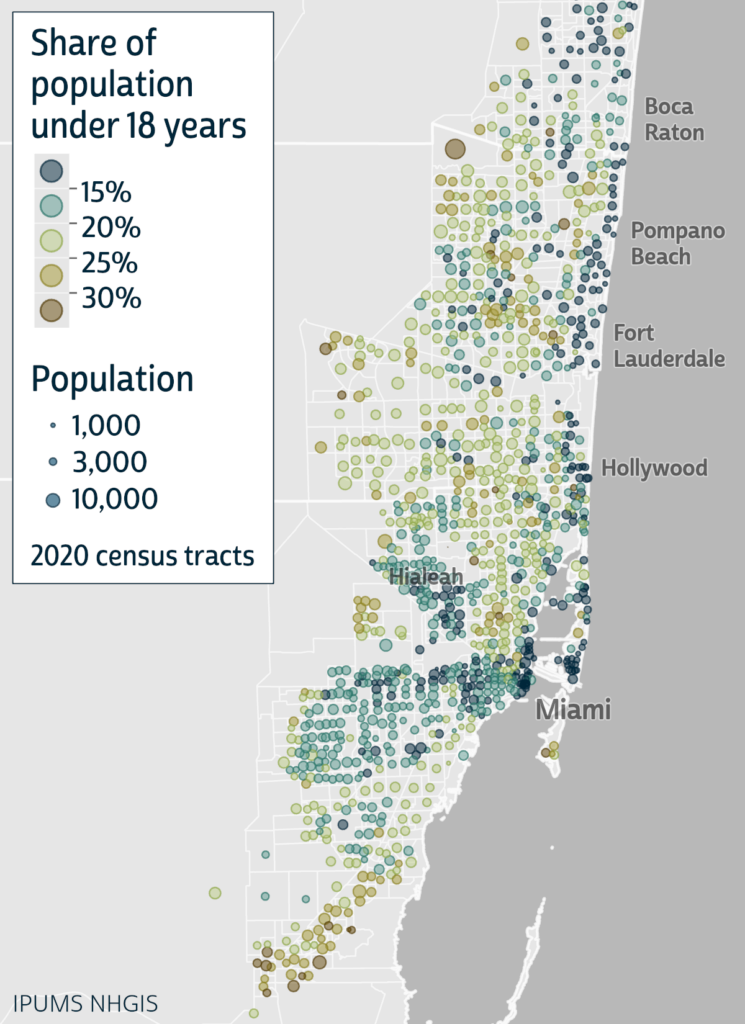
By Kari Williams & Isabel Pastoor

The U.S. Department of Agriculture (USDA) defines a household as being food secure when all household members at all times have access to “enough food for an active, healthy life;” it sets a minimum threshold for food security of “ready availability of nutritionally adequate and safe foods” and the “assured ability to acquire acceptable foods in socially acceptable ways” (USDA Economic Research Service, 2025). The USDA provides survey modules for assessing food security in the U.S. (see Table 1), which are used in a number of federal surveys.

Following the recent announcement by the USDA that they plan to cease data collection for the Food Security supplement fielded as part of the December Current Population Survey, we are highlighting data sources for studying food security in the U.S. Table 2 provides an overview of a number of federal data sources that can be used to study aspects of food security in the U.S. This list of data sources is not exhaustive; we have prioritized data available through IPUMS and other long-running and large-scale population surveys. Additional sources covering shorter time periods or more specific focal populations can be found from the USDA’s Food Security in the United States Documentation page and the Food Access Research Atlas.

Unlocking Spatial and Social Data with R: Introducing the R Spatial Notebook Series

May 14, 2025April 4, 2025 by mpcblog

By Kate Vavra-Musser

Introduction: What is the R Spatial Notebooks Project?

The R Spatial Notebooks Project is a series of R code notebooks, structured like a textbook, designed to guide users through the intricacies of data extraction, integration, cleaning, analysis, and visualization using R. The notebooks are specifically tailored for social science research and applications using spatial data. The modular textbook-style structure is designed for comprehensive skill development by working through sequences of notebooks. The project was developed through a partnership between the Institute for Social Research and Data Innovation (ISDRI), which houses IPUMS, and the Institute for Geospatial Understanding through an Integrated Discovery Environment (I-GUIDE). IPUMS provides census and survey data from around the world integrated across time and space. I-GUIDE is cyberinfrastructure that combines distributed geospatial data with computing for researchers, students, and policymakers.

The initial R Spatial Notebooks release includes roughly 20 freely-available notebooks on topics including IPUMS data extraction via API, accessing open-source data, data cleaning, foundational spatial data principles, exploratory data analysis, and mapping.

Updated Land Cover Summaries for Census Tracts, County Subdivisions, Counties, and Places

June 17, 2025December 2, 2024 by mpcblog

By David Van Riper, ISRDI Director of Spatial Analysis

What’s new?

We just released updated land cover summaries for census tracts, county subdivisions, counties and places. Our land cover summaries describe the proportion of a particular geographic unit (e.g., a county or a census tract) that is covered by a particular land cover class (e.g., deciduous forest, evergreen forest, or cultivated crops). This release provides users with land cover summaries from nine vintages of the National Land Cover Database (NLCD) – 2001, 2004, 2006, 2008, 2011, 2013, 2016, 2019, and 2021. Summaries are available for 2010, 2020, and 2022 census tract, county subdivisions, counties, and places. We include 2022 versions of these geographic units because that was the year the Census Bureau began identifying planning regions in Connecticut. These regions replaced Connecticut’s historical counties, which have long had no official administrative function. These new planning regions changed the unique identifiers for census tracts, county subdivisions, and counties.

Why did IPUMS NHGIS create these land cover summaries?

Land cover data is commonly used to study the impacts of natural events such as hurricanes or human modifications such as converting forest to agriculture or agricultural land to developed land. Land cover data is typically released as a high spatial resolution, gridded spatial dataset where each grid cell (or pixel) is assigned to a land cover category (Figure 1, Panel A). The gridded data almost never align with the geographic units, and the high spatial resolution yields massive files that can be slow to process. A single NLCD file is 25 gigabytes in size.

We summarized nine versions of the NLCD to multiple sets of geographic units so that users can easily integrate the data into analyses already structured around geographic units. This reduces the burden on individual users to create such summaries themselves.

Bivariate Proportional Symbol Maps, Part 2: Design Tips with Instructions for ArcGIS Pro

February 22, 2024February 22, 2024 by mpcblog

By Jonathan Schroeder, IPUMS Research Scientist, NHGIS Project Manager

How to make effective bivariate proportional symbol maps

A map of the share of population under age 18 in the Miami area in 2020. There is one colored circle for each census tract. There are five colors ranging from dark blue (representing less than 15% under age 18) to light green (representing 20 to 25% under age 18) to brown (representing 30% or more). The circle sizes correspond to tract populations. Most circles have similar sizes, representing around 1,000 to 10,000 people. The circles cluster together forming groups where there are more tracts and more people. The circles in central Miami and along the coast are bluer than elsewhere. — A bivariate proportional symbol map.
Click map for larger version.

In Part 1 of this blog series, I introduced bivariate proportional symbol maps and shared some examples to demonstrate their advantages. In short, when they’re well designed, they can make it easy to see multiple dimensions of a population all at once: size, composition, and spatial distribution.

A key part of that statement is, “when they’re well designed.” Standard mapping tools can make it easy to get started, but getting all the way to a good design still takes some extra effort.

In this Part 2 post, I discuss some key design considerations for bivariate proportional symbol maps, and I provide specific instructions to help you get to a good design.

Software considerations

I used Esri’s ArcGIS Pro to create the examples here and in Part 1. The design tips I share below should be relevant for any mapping tool, but my instructions are specifically for ArcGIS Pro (version 3.2). I expect there are ways to achieve similar designs with QGIS, R, Python, etc., quite possibly more easily than with ArcGIS Pro. I can only say that it’s easier to create effective bivariate proportional symbols now with ArcGIS Pro than it was with its predecessor ArcMap.

As I proceed, I’ll flag which instructions pertain specifically to ArcGIS Pro. All other tips are “tool neutral.”

General tip: Match size to “size” and color to “character”

When selecting which features to map, a framework that works consistently well is to use symbol color to represent an intensive property—e.g., the share of population under 18 years old, average household size, median household income, or the share of votes cast for a candidate—and use symbol size to represent the number of cases to which the intensive property pertains—e.g., the total population (when color corresponds to a population share) or the count of households (when color corresponds to average household size or median household income).

This framework enables the map to illustrate both the spatial distribution of the mapped characteristics and the frequency distribution of the intensive property—e.g., not only where a candidate received large or small vote shares but also how many votes were cast in each of those areas. Other frameworks can also work well (e.g., see the change maps in Part 1), but it’s generally very helpful if the two mapped characteristics relate to each other in a way that corresponds intuitively with “size” and “color.”

Bivariate Proportional Symbol Maps, Part 1: An Introduction

February 22, 2024February 7, 2024 by mpcblog

By Jonathan Schroeder, IPUMS Research Scientist, NHGIS Project Manager

A powerful, underused mapping technique

The world could use a lot more bivariate proportional symbol maps. These maps pair two basic visual variables—size and (usually) color—to symbolize two characteristics of mapped features. When designed well, they convey multiple key dimensions of a population all at once: size and composition as well as spatial distribution and density.

Unfortunately, standard mapping software hasn’t made it easy to create good versions of these maps, and most introductions to statistical mapping stick to simpler strategies. As a result, bivariate proportional symbols aren’t used very often. With few examples and little guidance to go on, it’s understandable that mapmakers don’t realize how often they’re a viable, well-suited option.

This two-part blog series aims to spark more interest by providing a “few examples” (Part 1) and a “little guidance” (Part 2).

Picking up where I left off

In a previous blog post, I shared an example of a bivariate proportional symbol map and described some of the technique’s advantages. But that post focuses on a mapping resource (census centers of population) rather than on mapping techniques. Most of the examples in the post are also simply “proportional symbol maps,” without the more intriguing “bivariate” part.

To close that post, I suggested “a tantalizing next step” would be to use bivariate proportional symbols with small-area data (for census tracts or block groups), and I shared a few technical notes and design tips without much detail. I later expanded on those ideas in a conference talk, sharing some new examples with small-area data and going a little deeper with design tips.

In these new posts, I’m sharing and building on the examples and tips from the conference talk.

Accessing IPUMS NHGIS in R: A Primer

June 13, 2025September 18, 2023 by mpcblog

By Finn Roberts & Jonathan Schroeder

R users have a powerful new way to access IPUMS NHGIS!

The July 2023 release of ipumsr 0.6.0 includes a fully-featured set of client tools enabling R users to get NHGIS data and metadata via the IPUMS API. Without leaving their R environment, users can find, request, download and read in U.S. census summary tables, geographic time series, and GIS mapping files for years from 1790 through the present. This blog post gives an overview of the possibilities and describes how to get started.

What you can do with ipumsr

Request and download NHGIS data

You can use ipumsr to specify the parameters of an NHGIS data extract request and submit that request for processing by the IPUMS servers. You can request any of the data products that are available through the NHGIS Data Finder: summary tables, time series tables, and shapefiles. You can also specify general formatting parameters (e.g., file format or time series table layout) to customize the structure of your data extract.

Once you have specified a data extract, you can use a series of ipumsr functions to:

submit the extract request to the IPUMS servers for processing
check on the extract status
wait for the extract to complete
download the extract as soon as it’s ready
load the data into R with detailed data field descriptions.

This workflow allows you to go from a set of abstract NHGIS data specifications to analyzable data, all without having to leave your R session!

Better Maps with Census Centers of Population

June 13, 2025February 17, 2022 by mpcblog

Jonathan Schroeder, IPUMS Research Scientist, NHGIS Project Manager

The best mapping resource no one’s using?

In the domain of U.S. population mapping, the Census Bureau’s centers of population may be the nation’s most underused data resource. Before I explain why, let’s cover some basics…

What are they? A center of population represents the mean location of residence for an area’s population, roughly the average latitude and longitude, adjusting for the curvature of the earth. For the last three decennial censuses (2000, 2010, 2020), the Census Bureau has published centers of population separately for U.S. states, counties, census tracts, and block groups.

Where can you get them? Through the Census Bureau website, you can download files containing the latitude and longitude coordinates for centers of population. To facilitate mapping and analysis, IPUMS NHGIS has transformed the coordinates into point shapefiles, available for download through the NHGIS Data Finder.

What are they used for? At the moment, not much! But there are dozens of settings where they’d be helpful. I’m hoping this blog will help get the word out, and if it does, you might now be reading this in some future age, marveling how we ever went so long without using them!

OK, how should we use them? In the case of statistical maps—my focus here—centers of population are wonderfully effective for placing proportional symbols. I share lots of examples down below to demonstrate, but first, let’s consider the general advantages of proportional symbol maps compared to a more common alternative: choropleth maps…